Из огромного многообразия всевозможных множеств особый интерес представляют так называемые числовые множества , то есть, множества, элементами которых являются числа. Понятно, что для комфортной работы с ними нужно уметь их записывать. С обозначений и принципов записи числовых множеств мы и начнем эту статью. А дальше рассмотрим, как числовые множества изображаются на координатной прямой.

Навигация по странице.

Запись числовых множеств

Начнем с принятых обозначений. Как известно, для обозначения множеств используются заглавные буквы латинского алфавита. Числовые множества, как частный случай множеств, обозначаются также. Например, можно говорить о числовых множествах A , H , W и т.п. Особую важность имеют множества натуральных, целых, рациональных, действительных, комплексных чисел и т.п., для них были приняты свои обозначения:

• N – множество всех натуральных чисел;
• Z – множество целых чисел;
• Q – множество рациональных чисел;
• J – множество иррациональных чисел;
• R – множество действительных чисел;
• C – множество комплексных чисел.

Отсюда понятно, что не стоит обозначать множество, состоящее, к примеру, из двух чисел 5 и −7 как Q , это обозначение будет вводить в заблуждение, так как буквой Q обычно обозначают множество всех рациональных чисел. Для обозначения указанного числового множества лучше использовать какую-нибудь другую «нейтральную» букву, например, A .

Раз уж мы заговорили про обозначения, то здесь напомним и про обозначение пустого множества, то есть множества, не содержащего элементов. Его обозначают знаком ∅.

Также напомним про обозначение принадлежности и непринадлежности элемента множеству. Для этого используют знаки ∈ - принадлежит и ∉ - не принадлежит. Например, запись 5∈N означает, что число 5 принадлежит множеству натуральных чисел, а 5,7∉Z – десятичная дробь 5,7 не принадлежит множеству целых чисел.

И еще напомним про обозначения, принятые для включения одного множества в другое. Понятно, что все элементы множества N входят в множество Z , таким образом, числовое множество N включено в Z , это обозначается как N⊂Z . Также можно использовать запись Z⊃N , которая означает, что множество всех целых чисел Z включает множество N . Отношения не включено и не включает обозначаются соответственно знаками ⊄ и ⊅. Также используются знаки нестрогого включения вида ⊆ и ⊇, означающие соответственно включено или совпадает и включает или совпадает.

Про обозначения поговорили, переходим к описанию числовых множеств. При этом затронем лишь основные случаи, которые наиболее часто используются на практике.

Начнем с числовых множеств, содержащих конечное и небольшое количество элементов. Числовые множества, состоящие из конечного числа элементов, удобно описывать, перечисляя все их элементы. Все элементы-числа записываются через запятую и заключаются в , что согласуется с общими правилами описания множеств . Например, множество, состоящее из трех чисел 0 , −0,25 и 4/7 можно описать как {0, −0,25, 4/7} .

Иногда, когда число элементов числового множества достаточно велико, но элементы подчиняются некоторой закономерности, для описания используют многоточие. Например, множество всех нечетных чисел от 3 до 99 включительно можно записать как {3, 5, 7, …, 99} .

Так мы плавно подошли к описанию числовых множеств, число элементов которых бесконечно. Иногда их можно описать, используя все тоже многоточие. Для примера опишем множество всех натуральных чисел: N={1, 2. 3, …} .

Также пользуются описанием числовых множеств посредством указания свойств его элементов. При этом применяют обозначение {x| свойства} . Например, запись {n| 8·n+3, n∈N} задает множество таких натуральных чисел, которые при делении на 8 дают остаток 3 . Это же множество можно описать как {11,19, 27, …} .

В частных случаях числовые множества с бесконечным числом элементов представляют собой известные множества N , Z , R , и т.п. или числовые промежутки. А в основном числовые множества представляются как объединение составляющих их отдельных числовых промежутков и числовых множеств с конечным числом элементов (о которых мы говорили чуть выше).

Покажем пример. Пусть числовое множество составляют числа −10 , −9 , −8,56 , 0 , все числа отрезка [−5, −1,3] и числа открытого числового луча (7, +∞) . В силу определения объединения множеств указанное числовое множество можно записать как {−10, −9, −8,56}∪[−5, −1,3]∪{0}∪(7, +∞) . Такая запись фактически означает множество, содержащее в себе все элементы множеств {−10, −9, −8,56, 0} , [−5, −1,3] и (7, +∞) .

Аналогично, объединяя различные числовые промежутки и множества отдельных чисел, можно описать любое числовое множество (состоящее из действительных чисел). Здесь становится понятно, почему были введены такие виды числовых промежутков как интервал, полуинтервал, отрезок, открытый числовой луч и числовой луч: все они в купе с обозначениями множеств отдельных чисел позволяют описывать любые числовых множества через их объединение.

Обратите внимание, что при записи числового множества составляющие его числа и числовые промежутки упорядочиваются по возрастанию. Это не обязательное, но желательное условие, так как упорядоченное числовое множество проще представить и изобразить на координатной прямой. Также отметим, что в подобных записях не используются числовые промежутки с общими элементами, так как такие записи можно заменить объединением числовых промежутков без общих элементов. Например, объединение числовых множеств с общими элементами [−10, 0] и (−5, 3) есть полуинтервал [−10, 3) . Это же относится и к объединению числовых промежутков с одинаковыми граничными числами, например, объединение (3, 5]∪(5, 7] представляет собой множество (3, 7] , на этом мы отдельно остановимся, когда будем учиться находить пересечение и объединение числовых множеств .

Изображение числовых множеств на координатной прямой

На практике удобно пользоваться геометрическими образами числовых множеств – их изображениями на . Например, при решении неравенств , в которых необходимо учитывать ОДЗ, приходится изображать числовые множества, чтобы найти их пересечение и/или объединение. Так что полезно будет хорошо разобраться со всеми нюансами изображения числовых множеств на координатной прямой.

Известно, что между точками координатной прямой и действительными числами существует взаимно однозначное соответствие, что означает, что сама координатная прямая представляет собой геометрическую модель множества всех действительных чисел R . Таким образом, чтобы изобразить множество всех действительных чисел, надо начертить координатную прямую со штриховкой на всем ее протяжении:

А часто даже не указывают начало отсчета и единичный отрезок: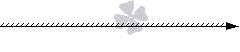

Теперь поговорим про изображение числовых множеств, представляющих собой некоторое конечное число отдельных чисел. Для примера, изобразим числовое множество {−2, −0,5, 1,2} . Геометрическим образом данного множества, состоящего из трех чисел −2 , −0,5 и 1,2 будут три точки координатной прямой с соответствующими координатами: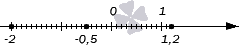

Отметим, что обычно для нужд практики нет необходимости выполнять чертеж точно. Часто достаточно схематического чертежа, что подразумевает необязательное выдерживание масштаба, при этом важно лишь сохранять взаимное расположение точек относительно друг друга: любая точка с меньшей координатой должна быть левее точки с большей координатой. Предыдущий чертеж схематически будет выглядеть так: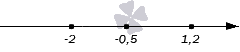

Отдельно из всевозможных числовых множеств выделяют числовые промежутки (интервалы, полуинтервалы, лучи и т.д.), что представляют их геометрические образы, мы подробно разобрались в разделе . Здесь не будем повторяться.

И остается остановиться лишь на изображении числовых множеств, представляющих собой объединение нескольких числовых промежутков и множеств, состоящих из отдельных чисел. Здесь нет ничего хитрого: по смыслу объединения в этих случаях на координатной прямой нужно изобразить все составляющие множества данного числового множества. В качестве примера покажем изображение числового множества (−∞, −15)∪{−10}∪[−3,1)∪ {log 2 5, 5}∪(17, +∞) :

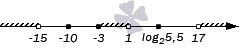
И остановимся еще на достаточно распространенных случаях, когда изображаемое числовое множество представляет собой все множество действительных чисел, за исключением одной или нескольких точек. Такие множества частенько задаются условиями типа x≠5 или x≠−1 , x≠2 , x≠3,7 и т.п. В этих случаях геометрически они представляют собой всю координатную прямую, за исключением соответствующих точек. Иными словами, из координатной прямой нужно «выколоть» эти точки. Их изображают кружочками с пустым центром. Для наглядности изобразим числовое множество, соответствующее условиям (это множество по сути есть ):

Подведем итог. В идеале информация предыдущих пунктов должна сформировать такой же взгляд на запись и изображение числовых множеств, как и взгляд на отдельные числовые промежутки: запись числового множества сразу должна давать его образ на координатной прямой, а по изображению на координатной прямой мы должны быть готовы с легкостью описать соответствующее числовое множество через объединение отдельных промежутков и множеств, состоящих из отдельных чисел.

Список литературы.

• Алгебра: учеб. для 8 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. - 16-е изд. - М. : Просвещение, 2008. - 271 с. : ил. - ISBN 978-5-09-019243-9.
• Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. - 13-е изд., стер. - М.: Мнемозина, 2011. - 222 с.: ил. ISBN 978-5-346-01752-3.

Условные обозначения, предназначенные для записи математич. понятий и выкладок. Напр., понятие "квадратный корень из числа, равного отношению длины окружности к ее диаметру" обозначается кратко а предложение "отношение длины окружности к ее диаметру больше, чем три и десять семьдесят первых, и меньше, чем три и одна седьмая" записывается в виде:

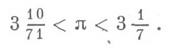
Развитие математической символики было тесно связано с общим развитием понятий и методов математики.

Первыми 3. м. были знаки для изображения чисел - цифры, возникновение которых, по-видимому, предшествовало введению письменности. Наиболее древние системы нумерации (системы счисления )- вавилонская и египетская - возникли еще за тысячелетия до н. э.

Первые 3. м. для произвольных величин появились много позднее (начиная с 5-4 вв. до н. э.) в Греции. Произвольные величины (площади, объемы, углы) изображались в виде отрезков, а произведение двух произвольных величин - в виде прямоугольника, построенного на соответствующих отрезках. В "Началах" Евклида (3 в. до н. э.) величины обозначаются двумя буквами - начальной и конечной буквами соответствующего отрезка, а иногда и одной. У Архимеда (3 в. до н. э.) последний способ обозначения становится обычным. Подобное обозначение содержало в себе возможности развития буквенного исчисления. Однако в классической античной математике над буквами никаких операций не производилось, а буквенного исчисления создано не было.

Начатки буквенного обозначения и исчисления возникают в позднеэллинистич. эпоху в результате освобождения алгебры от геометрич. формы. Диофант (вероятно, 3 в.) обозначал неизвестную (х)и ее степени следующими знаками:

(- от греч. термина обозначавшего квадрат неизвестной,- от греч. - куб). Справа от неизвестной или ее степеней Диофант писал коэффициенты, напр. Зх 5 обозначалось (где ). При сложении Диофант приписывал слагаемые друг к другу, при вычитании употреблял специальный знак ; равенство Диофант обозначал буквой i (от греч. isoc - равный). Напр., уравнение

(x 3 +8x)-(5x 2 -1)=x у Диофанта записалось бы так:

(здесь а означает, что единица не имеет множителя в виде степени неизвестного).

Несколько веков спустя индийцы, разрабатывавшие числовую алгебру, ввели различные 3. м. для нескольких неизвестных (сокращения наименований цветов, обозначавших неизвестные), квадрата, квадратного корня, вычитаемого числа. Так, уравнение

3 х 2 +10х- 8=x 2 +1

в записи Брахмагупты (7 в.) имело бы вид:

(йа - от йават - тават - неизвестное, ва - от варга - квадратное число, ру - от рупа - монета рупия - свободный член, точка над числом означает вычитаемое число).

Создание современной алгебраич. символики относится к 14-17 вв.; оно определялось успехами практич. арифметики и учения об уравнениях. В различных странах стихийно появляются 3. м. для нек-рых действий и для степеней неизвестной величины. Проходят многие десятилетия и даже века, прежде чем вырабатывается тот или иной удобный для исчисления символ. Так, в конце 15 в. Н. Шюке (N. Chuquet) и Л. Пачоли (L. Pacioli) употребляли знаки сложения и вычитания р и ш (от. лат. plus и minus), немецкие математики ввели современные + (вероятно, сокращение лат. et) и - . Еще в 17 в. можно насчитать около десятка 3. м. для действия умножения:

Поучительна история знака радикала. Вслед за Леонардо Пизанским (Leonardo Pisano, 1220) многие обозначали (вплоть до 17 в.) квадратный корень знаком (от лат. radix - корень). Н. Шюке обозначал квадратный, кубический и т. д. корни знаками и т. д. В немецкой рукописи ок. 1480 квадратный корень обозначался точкой перед числом, кубич. корень- тремя точками, а корень четвертой степени - двумя точками. У К. Рудольфа (Ch. Rudolff, 1525) корень уже обозначался . Для обозначения корней высших степеней различные ученые то пишут этот знак несколько раз подряд, то ставят после него букву - сокращение наименования показателя, то - соответствующую цифру в кружке или с круглой или квадратной скобкой, чтобы отделить ее от подрадикального числа [горизонтальную черту над подрадикальным выражением ввел Р. Декарт (R. Descartes), 1637], и лишь в начале 18 в. входит в обиход запись показателя корня вверху над отверстием знака радикала, встречающаяся ранее у А. Жирара (A. Girard, 1629). Таким образом, эволюция знака радикала длилась почти пятьсот лет.

Весьма различны были 3. м. неизвестной и ее степеней. В 16 и начале 17 вв. конкурировало более десяти обозначений для одного только квадрата неизвестной, напр, се (от census - лат. термин, служивший переводом греч. Q (от quadratum),A (2), 1 2 , А ii , аа, а 2 и т. д. Так, уравнение х 3 +5x=12 имело бы у Дж. Кардано (G. Cardano, 1545) вид:

(cubus- куб, positio - неизвестная, oequantur - равно);

у М. Штифеля (М. Stifel, 1544):

у Р. Бомбелли(R. Bombelli, 1572):

Куб неизвестной, - неизвестная; eguale - равно); у Ф. Виета (F. Viete, 1591):

(С - cubus - куб, N - numerus - число); у Т. Гарриота (Т. Harriot, 1631):

В 16 и начале 17 вв. входят в употребление знаки равенства и скобки: квадратные (Р. Бомбелли, 1550), круглые (Н. Тарталья, N. Tartaglia, 1556), фигурные (Ф. Виет, 1593).

Значительным шагом вперед в развитии математич. символики явилось введение Ф. Виетом (1591) 3. м. для произвольных постоянных величин в виде прописных согласных букв латинского алфавита В, D, что дало ему возможность впервые записывать алгебраич. уравнения с произвольными коэффициентами и оперировать с ними. Неизвестные Ф. Виет обозначал гласными прописными буквами А, Е, ... . Напр., запись Ф. Виета

в наших символах выглядит так:

x 3 + 3bx = d.

Ф. Виет явился творцом алгебраич. формул. Р. Декарт (1637) придал знакам алгебры современный вид, обозначая неизвестные последними буквами латинского алфавита х, у, z, а произвольные данные величины - начальными буквами а, b, с. Ему же принадлежит нынешнее обозначение степени. Обозначения Р. Декарта обладали большим преимуществом по сравнению со всеми предыдущими. Поэтому они скоро получили всеобщее признание.

Дальнейшее развитие 3. м. было тесно связано с созданием анализа бесконечно малых, для разработки символики к-рого основа была уже в большой мере подготовлена в алгебре. И. Ньютон (I. Newton) в своем методе флюксий и флюент (1666 и следующие годы) ввел знаки для последовательных флюксий (производных) величины хв виде и для бесконечно малого приращения о. Несколько ранее Дж. Валлис (J. Wallis, 1655) предложил знак бесконечности оо. Создателем современной символики дифференциального и интегрального исчислений является Г. Лейбниц (G. Leibniz). Ему, в частности, принадлежат употребляемые ныне З. м. дифференциалов dx, d 2 x, d 3 x и интеграла

Следует подчеркнуть принципиальное преимущество знака интеграла, данного Г. Лейбницем, перед предложенным И. Ньютоном знаком х. В знаке Г. Лейбница отражающем самый процесс построения интегральной суммы, явно указана и интегрируемая функция и переменная интегрирования. Благодаря этому знак годится и для записи формул замены переменных и легко может быть использован для записи кратных и криволинейных интегралов. Знак И. Ньютона " х таких возможностей непосредственно не представляет. Аналогично обстоит дело с лейбницевыми знаками дифференциалов и ньютоновыми знаками флюксий и бесконечно малого приращения. --Огромная заслуга в создании символики современной математики принадлежит Л. Эйлеру (L. Euler). Он ввел в общее употребление первый знак переменной операции, именно знак функции f(x)(от лат. functio - функция, 1734). Несколько ранее знак jx был применен И. Бернулли (J. Bernoulli, 1718). После работ Л. Эйлера знаки для многих индивидуальных функций, напр, тригонометрических, приобрели стандартный характер. Л. Эйлеру же принадлежат обозначения постоянных е(основание натуральных логарифмов, 1736), p (вероятно, от греч.- окружность, периферия, 1736), мнимой единицы (от франц. imaginaire - мнимый, 1777, опубликовано в 1794), к-рые стали общеупотребительными.

В 19 в. роль символики еще более возрастает и, наряду с созданием новых 3. м., математики стремятся к стандартизации основных символов. Некоторые широко употребительные ныне 3. м. появляются лишь в это время: знак абсолютной величины | х| (К. Вейерштрасс, К. Weierstrass, 1841), вектора (О. Коши, A. Cauchy, 1853), определителя (А. Кэли, A. Cayley, 1841) и др. Многие теории, возникшие в 19 в., напр, тензорное исчисление, не могли быть развиты без подходящей символики. Характерно при этом увеличение удельного веса 3. м. для отношений, напр., сравнимости (К. Гаусс, С. Gauss, 1801), принадлежности изоморфизма эквивалентности и т. д. Знаки переменных отношений появляются с развитием математич. логики, особенно широко применяющей 3. м.

С точки зрения математической логики, среди 3. м. можно наметить следующие основные группы: А) знаки объектов, Б) знаки операций, В) знаки отношений. Например, знаки 1, 2, 3, 4 изображают числа, т. е. объекты, изучаемые арифметикой. Знак операции сложения + сам по себе не изображает никакого объекта; он получает предметное содержание лишь тогда, когда указано, какие числа складываются: запись 1+3 изображает число 4. Знак > (больше) есть знак отношения между числами. Знак отношения получает вполне определенное содержание, когда указано, между какими объектами отношение рассматривается. К указанным трем основным группам 3. м. примыкает еще четвертая: Г) вспомогательные знаки, устанавливающие порядок сочетания основных знаков. Достаточное представление о таких знаках дают скобки, указывающие порядок производства арифметич. действий.

Знаки каждой из трех групп А), Б) и В) бывают двух родов: 1) индивидуальные знаки вполне определенных объектов, операций и отношений, 2) общие знаки "переменных", или "неизвестных", объектов, операций и отношений. Примерами знаков первого рода могут служить (см. также таблицу на кол. 462, 463):

А 1) Обозначения натуральных чисел 1, 2, 3, 4, 5, 6, 7, 8, 9; трансцендентных чисел еи я; мнимой единицы и т. п.

Б 1) Знаки арифметич. действий +, -, Х, , : ; извлечения корня дифференцирования d/dx, оператора Лапласа

Сюда же относятся знаки индивидуальных функций sin, tg, log и т. п.

B 1 )Знаки равенства и неравенства =, >, <, знаки параллельности || и перпендикулярности и т. п.

Знаки второго рода изображают произвольные объекты, операции и отношения определённого класса или объекты, операции и отношения, подчиненные к.-л. заранее оговоренным условиям. Напр., при записи тождества

( а+b )( а-b ) = а 2 -b 2

буквы а и 6 обозначают произвольные числа; при изучении"функциональной зависимости

буквы х и у изображают произвольные числа, связанные заданным отношением; при решении уравнения

хобозначает любое число, удовлетворяющее данному уравнению (в результате решения этого уравнения мы узнаем, что этому условию соответствуют лишь два возможных значения +1 и -1).

С логич. точки зрения вполне законно все такого рода общие знаки наз. знаками переменных, как это принято в математич. логике ("область изме-

Даты возникновения некоторых математических знаков
	Значение		Когда введен
Знаки индивидуальных операций
	бесконечность	Дж. Валлис (J. Wallis)
	основание натуральных логарифмов	Л. Эйлер (L. Euler)
	отношение длины окружности к диаметру	У. Джонс (W. Jones) Л. Эйлер (L. Euler)
	корень квадратный из -1	Л. Эйлер (L. Euler)	1777 (в печати 1794)
	единичные векторы, орты	У. Гамильтон (W. Hamilton)
	угол параллельности	Н. И. Лобачевский
Знаки переменных объектов
х, у, z	неизвестные или переменные величины	Р. Декарт (R. Descartes)
Знаки индивидуальных операций
	сложение вычитание	немецкие математики	конец 15 в.
	умножение	У. Оутред (W. Oughtred)
	умножение	Г. Лейбниц (G. Leibniz)
		Г. Лейбниц
a 2 , а 3 ,..., а n		Р. Декарт (R. Descartes) И. Ньютон (I. Newton)
		К. Рудольф (К. Rudolf) А. Жирар (A. Girard)
	логарифм	И. Кеплер (J. Kepler) Б. Кавальери (B. Cavalieri)
	синус косинус тангенс	Л. Эйлер (L. Euler) Л. Эйлер
	арксинус	Ж. Лагранж
	гиперболический синус гиперболический косинус	В. Риккати (V. Riccati)
dx,ddx,..., d 2 x,d 3 x,...	дифференциал	Г. Лейбниц (G. Leibniz)	1675 (в печати
	интеграл	Г. Лейбниц (G. Leibniz)	1675 (в печати 1686)
	производная	Г. Лейбниц (G. Leibniz)
f" (x),y",f"x	производная	Ж. Лагранж (J. Lagrange)
	разность, приращение	Л. Эйлер (L. Euler)
	частная производная	А. Лежандр (A. Legendre)
	определенный интеграл	Ж. Фурье (J. Fourier)
		Л. Эйлер (L. Euler)
	произведение	К. Гаусс (С. Gauss)
	факториал	К. Крамп (Ch. Kramp)
		К. Вейерштрасс (К. Weierstrass),
		С. Люилье (S. L"Huillier) У. Гамильтон (W. Hamilton), многие математики	начало 20 в.

Продолжение
	Значение		Когда введен
	дзета-функция	Б. Риман (В. Rlemann)
	гамма-функция	А. Лежандр (A. Legendre)
	бета-функция	Ж. Бине (J. Binet)
	дельта (оператор Лапласа)	Р. Мёрфи (R. Murphy)
	набла (оператор Гамильтона)	У. Гамильтон (W. Hamilton)
Знаки переменных операций
		И. Бернулли (J. Bernoulli) Л. Эйлер (L. Euler)
Знаки индивидуальных отношений
	равенство	Р. Рекорд (R. Recorde)
	больше меньше	Т. Гарриот (Т. Harriot)
	сравнимость	К. Гаусс (С. Gauss)
	параллельность	У. Оутред (W. Oughtred)	1677 (в посмертном издании)
	перпендикулярность	П. Эригон (P. Herigone)

нения" переменного может оказаться состоящей из одного единственного объекта или даже "пустой", напр., в случае уравнений, не имеющих решения). Дальнейшими примерами такого рода знаков могут служить:

А 2) Обозначения точек, прямых, плоскостей и более сложных геометрич. фигур буквами в геометрии.

Б 2) Обозначения f, F, j для функций и обозначения операторного исчисления, когда одной буквой Lобозначают, напр., произвольный оператор вида:

Обозначения для "переменных отношений" менее распространены; они находят применение лишь в математич. логике и в сравнительно абстрактных, по преимуществу аксиоматических, математич. исследованиях.

Лит. : Саjоri F., A history of mathematical notations, V. 1-2, Chi., 1928 - 29.

Warning : Invalid argument supplied for foreach() in /var/www/ravil1/data/www/wikireading.ru/views/slovar_glava.php on line 388

"ЗНАКИ МАТЕМАТИЧЕСКИЕ" в книгах

Математические науки

Из книги Повседневная жизнь Флоренции во времена Данте автора Антонетти Пьер

Математические науки Собственный вклад флорентийцев в средневековую теоретическую математику был незначительным и относился уже к эпохе более поздней, нежели эпоха Данте. Так, Паоло Дагомари (1281–1365) опубликовал «Трактат об абаке» (отсюда его прозвище: Паоло-Абако).

Знаки судьбы – это предупреждения? Могут ли темные силы путать человека, посылая свои знаки, сбивать с пути?

Из книги Судьбу можно изменить! Тайны Небесных Ангелов автора Панова Любовь

Знаки судьбы – это предупреждения? Могут ли темные силы путать человека, посылая свои знаки, сбивать с пути? Знаки судьба посылает, конечно, для того, чтобы предупредить. И посылает их нам не кто иной, как наши Ангелы-Хранители. Зачем? Чтобы ответить на этот вопрос, сначала

Б. МАТЕМАТИЧЕСКИЕ ТЕОРИИ

Из книги Загадки египетских пирамид автора Лауэр Жан-Филипп

Б. МАТЕМАТИЧЕСКИЕ ТЕОРИИ Источником возникновения некоторых математических теорий послужил, вероятнее всего, труд Жомара «Изложение системы мер древних египтян»225. Мы не будем возвращаться к основным астрономическим цифровым соотношениям, которые он стремится извлечь

Из книги Правила русской орфографии и пунктуации. Полный академический справочник автора Лопатин Владимир Владимирович

ЗНАКИ ПРЕПИНАНИЯ В КОНЦЕ И В НАЧАЛЕ ПРЕДЛОЖЕНИЯ. КОНЕЧНЫЕ ЗНАКИ В СЕРЕДИНЕ ПРЕДЛОЖЕНИЯ Знаки препинания в конце предложения § 1. В зависимости от цели сообщения, наличия или отсутствия эмоциональной окраски высказывания в конце предложения ставится точка

Папирусы математические

Из книги Большая Советская Энциклопедия (ПА) автора БСЭ

Таблицы математические

Из книги Большая Советская Энциклопедия (ТА) автора БСЭ

Математические журналы

Из книги Большая Советская Энциклопедия (МА) автора Автор неизвестен

12. ИНФОРМАЦИОННЫЕ ЗНАКИ И ЗНАКИ СООТВЕТСТВИЯ Информационные знаки – условные обозначения, предназначенные для оценки свойств и идентификации характеристик товара.Информационным знаки уведомляют:1.) о предприятии (фирме) – изготовителе (товарные знаки и знаки

Глава 18 Знаки будущего, знаки времени

Из книги Путь наименьшего сопротивления автора Фритц Роберт

Глава 18 Знаки будущего, знаки времени Многие убеждены, что мир на грани катастрофы. Государств, обладающих ядерным оружием, становится больше, насилие над природой вершится повсеместно, экстремизм растет, проблемы в экономике углубляются. Можно сказать,

Похожие статьи

Анализ текста повести «Очарованный странник

Minecraft PE теперь и на Windows Phone

Удаление папилломы кондиломы Кондиломы у женщин к какому врачу обращаться

Новообразования в ротовой полости у человека